Binary Search
Computer Science, , 2022
Let’s first talk about “Binary Search”. Just to be clear, in data structure, we also have “Binary Search Tree”. In Leetcode problems, a lot of seemingly hard problems can be solved efficiently (time complexity and space complexity wise) by Binary Search. Beccause the time complexity of Binary Search is $\quad O(\log n) $. For instance, if we have an array of length $\quad 2^{31} -1 $, then Binary Search will only traverse 31 times to find the number we want. Imagine how long it will take from a linear scan ! The most difficult part using Binary Search to solve problems is (1) when to use Binary Search and (2) if we can use it, how to transform the original problems into forms that we can easily visualize solutions using Binary Search. While the concept behind Binary Search is simple, writing a bug free algorithm is rather tricky. Let’s take a look at a Leetcode problem.
Leetcode Problem #704 - Binary Search
def BinarySearch(nums, target):
# nums is an array and target is a number we hope to find. If the target exists, then we return its index number
# If the number doesn't exist, we return -1
# nums must be sorted. If nums is not sorted, we sort it first.
low, high = 0, len(nums) - 1
while low < high:
mid = low + (high - low) // 2
# To prevent overflow
if nums[mid] < target:
# In this case, our search space lies to the right portion of mid.
low = mid + 1
elif nums[mid] > target :
high = mid
else:
return mid
# if we can't find the number, we return -1
if nums[low] == target:
return low
else:
return -1 Graphical explanation of Binary Search.
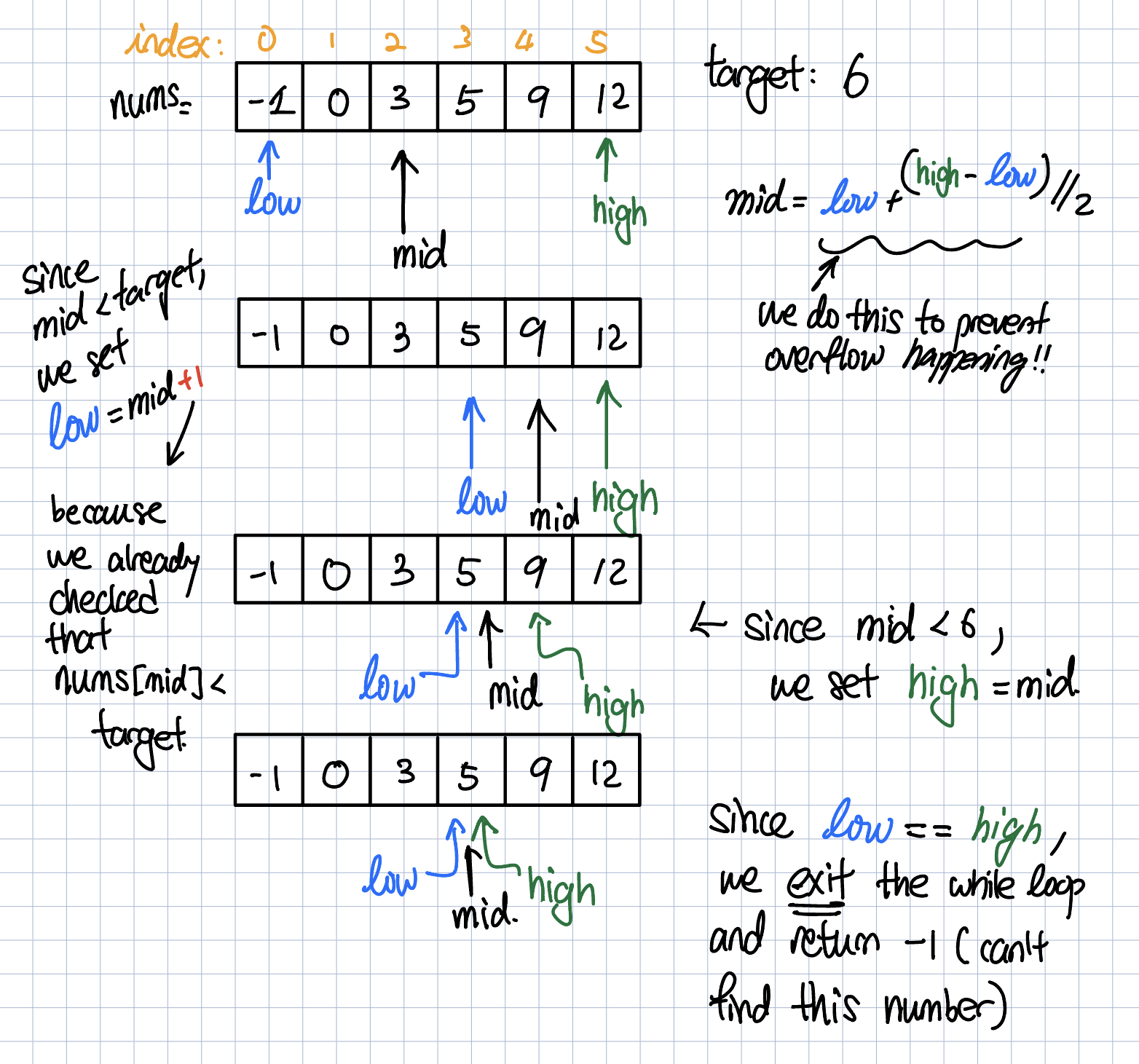
In addition to the overflow problem, you have to be careful about the condition in the While loop. Here, we have strictly less ( low < high). In some cases, you may see (low <= high). If you use “low <= high” in the code above and do not modify anything else, this code will not return the answer (or get stuck in the loop). So, if the condition in the while loop is (low <= high), then the following code works. Notice that we have “high = mid + 1” instead of “high = mid”.
def BinarySearch(nums, target):
# nums is an array and target is a number we hope to find. If the target exists, then we return its index number
# If the number doesn't exist, we return -1
# nums must be sorted. If nums is not sorted, we sort it first.
low, high = 0, len(nums) - 1
while low <= high:
mid = low + (high - low) // 2
# To prevent overflow
if nums[mid] < target:
# In this case, our search space lies to the right portion of mid.
low = mid + 1
elif nums[mid] > target :
high = mid - 1
else:
return mid
# if we can't find the number, we return -1
return -1 ======
Leetcode Problem #33 - Search in Rotated Sorted Array.
Here is the problem. Well, since the time complexity for this problem must be in $O(\log n)$, we can use Binary Search. However, we have rotation happening in this array. My approach was a bit more intuitive than the model solutions in the problem. We use Binary Search to find the rotation index.
Leetcode Problem #702 - Search in a Sorted Array of Unknown Size
Here is the problem. This one isn’t that much different from the previous problem. The difference is that we have an array of unknown size. However, the solution for this problem is very similar to the one we have seen so far. So what are our “low” and “high”? “low” would be 0. How about “high”? We can use While loop to find a reasonable value of “high”. See the code below for an implementation.
class ArrayReader:
def get(self, index: int) -> int:
class Solution:
def search(self, reader: 'ArrayReader', target: int) -> int:
low = 0
# let's find high
high_val = reader.get(0)
high = 1
while high_val < target:
high = high * 2
high_val = reader.get(high)
def BinarySearch(low, high):
while low < high:
mid = low + (high - low) // 2
mid_value = reader.get(mid)
if mid_value < target:
low = mid + 1
elif mid_value > target:
high = mid
else:
return mid
if reader.get(low) == target:
return low
else:
return -1
# This is another version of Binary Search
# while low <= high:
# mid = low + (high - low) // 2
# mid_value = reader.get(mid)
# if mid_value < target:
# low = mid + 1
# elif mid_value > target:
# high = mid - 1
# else:
# return mid
# return -1
return BinarySearch(0, high)Leetcode problem #1533 - Find the index of the larger Integer
We will use the binary search to solve this problem. However, we have to be a bit careful in this case, because we don’t have direct access to the given array.
Points to consider
- Notice that for an array with even length, even though reader.compareSub( ) has 3 possible values, it can’t have 0 as its output in this case.
- If our array has an odd length, then reader.compareSub( ) will not include the middle point, because we want to compare the sums of intervals with equal number of elements in them. For an even length, we don’t have to worry about this part. Furthermore, for an odd length, if reader.compareSub( ) returns 0, this means array[mid] is the maximum value in the array so we return this index mid.
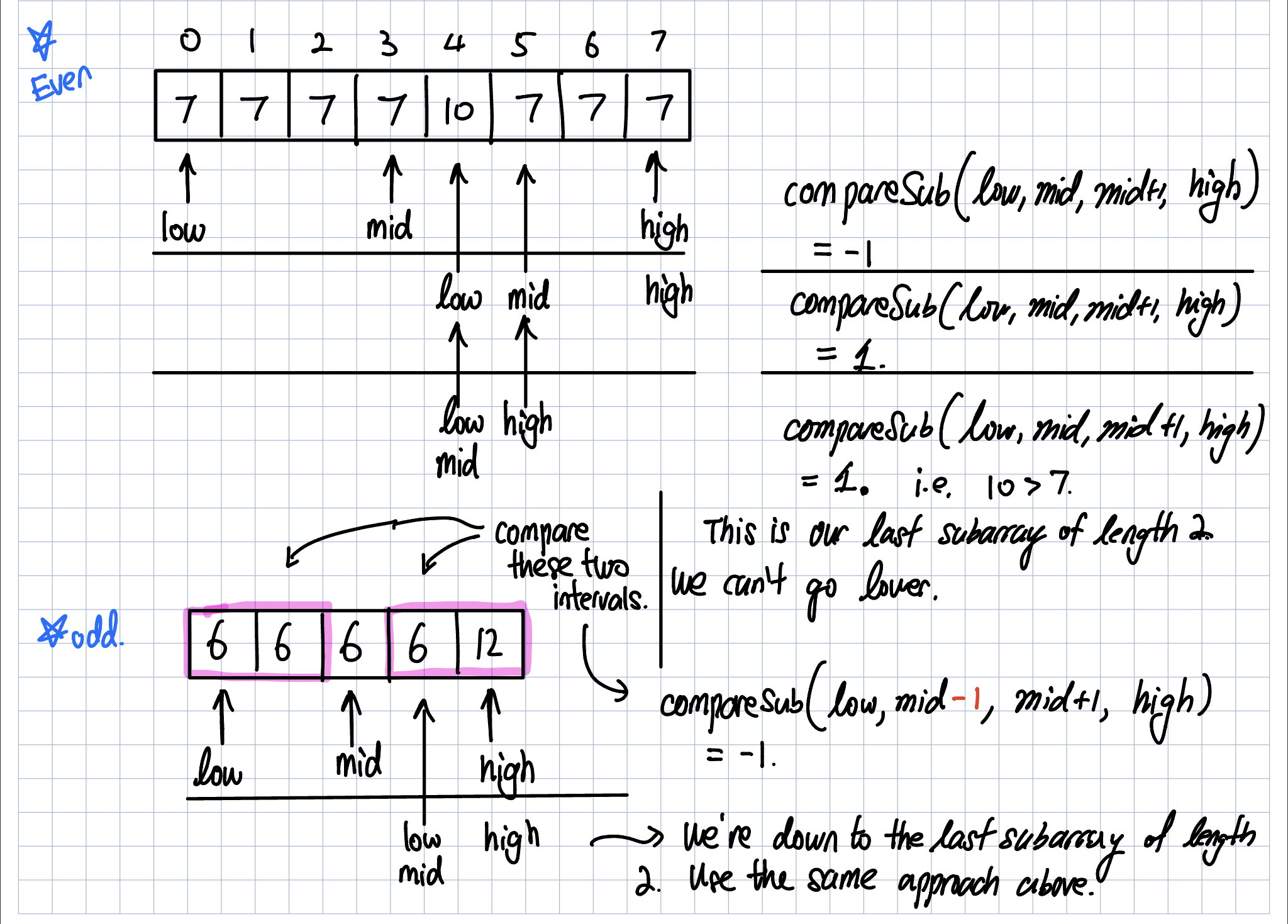
- When we are running binary search, it will eventually come down to a subarray of length 2. In this case, there are 2 cases to consider. If array[low] < array[high], then reader.compareSub(low, mid, mid + 1, high) will return -1 (in this case, low == mid and mid + 1 == high, since there are 2 elements). Similarly, if array[low] > array[high], then reader.compareSub(low, mid, mid + 1, high) will return 1. Now, notice that our While loop has a condition “low < high”. So when we update either low or high by mid + 1 or mid respectively, we will get kicked out of While loop, for failing to meet that condition. Therefore, we check beforehand to see if we are down to 2 elements in our subarray. A simple check like “if low + 1 == high” suffices. Then we return either low or high, depending on our condition. See the code for clarification.
class Solution:
def getIndex(self, reader: 'ArrayReader') -> int:
n = reader.length()
low, high = 0, n - 1
while low < high:
mid = low + (high - low) // 2
if mid - low + 1 != high - (mid + 1) + 1:
# odd case
result = reader.compareSub(low, mid - 1, mid + 1, high)
if result == 0:
return mid
elif result == 1:
high = mid
else:
low = mid + 1
if low == high:
return low
else:
# even case
result = reader.compareSub(low, mid, mid + 1, high)
if result == 1:
if low + 1 == high:
return low
high = mid
elif result == -1:
if low + 1 == high:
return high
low = mid + 1
Here’s my visual explanation.
Leetcode problem #1201 - Ugly Number 3
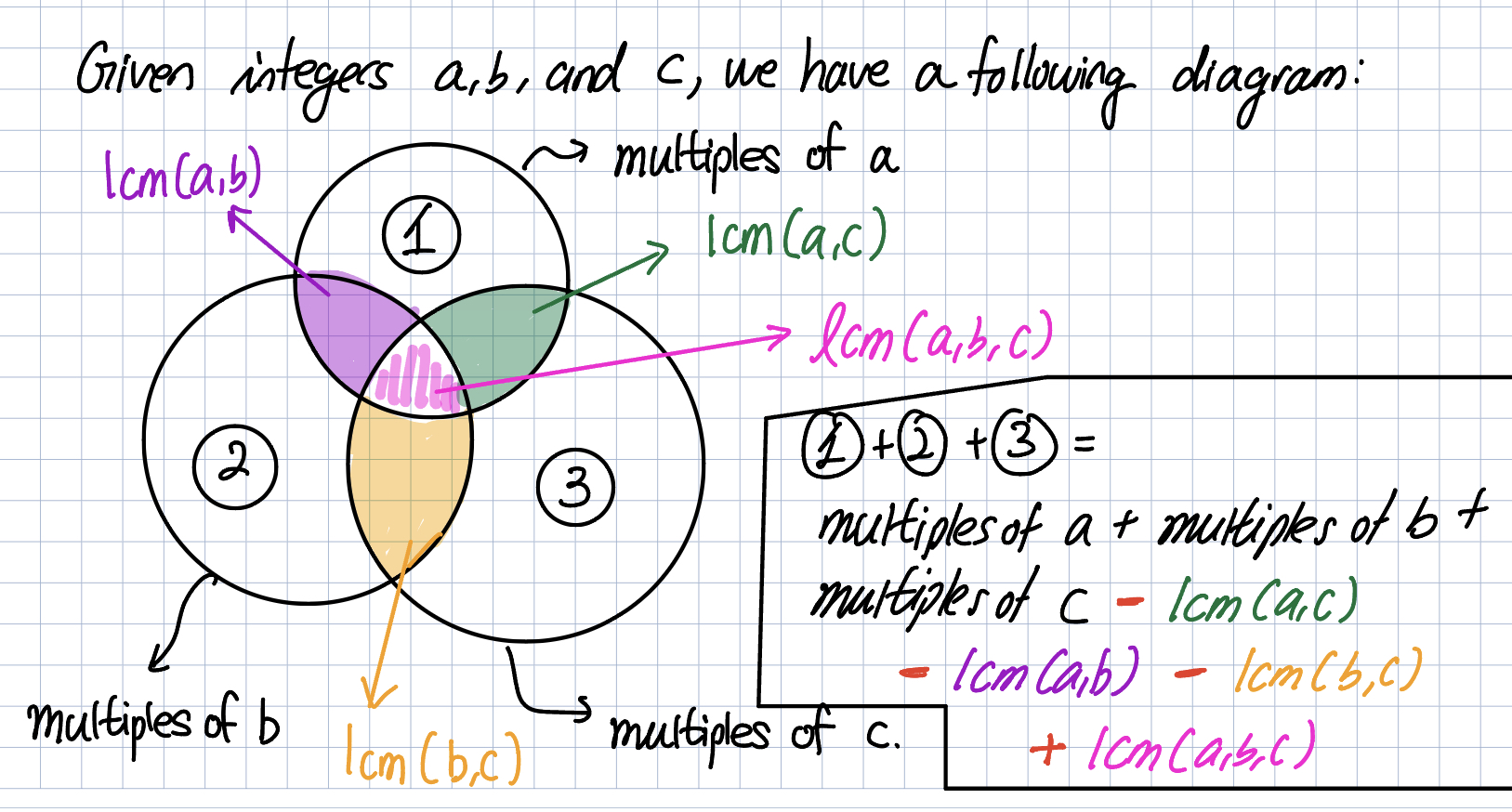
So the problem states that our number $n$ is less than or equal to $10^9$. This problem requires us to use least commom multiple (LCM) and greatest common divisor(GCD). Before we use these concepts, say we are given integers 3,4 and 5, and we want to find the 7th number that’s divisible by those 3 integers. How do we generate these numbers? Let’s pick a number 10 and see how many integers are divisible by those 3 integers. For an integer 2, these are the numbers that are less than or equal to 10, and are multiples of 2 : 2, 4, 6, 8, and 10. Similarly, for an integer 3, we have 3, 6 and 9. For 5, we have 5 and 10. We notice that there are duplicate numbers - 6 and 10. Well, 6 is a multiple of 2 and 3, and 10 is a multiple of 2 and 5. So we will use LCM to take care of duplicate numbers. Lastly, because we are given 3 integers, there will be integers multiple of those 3 integers. We actually have to add the numbers obtained from multiple of LCM of those 3 integers. It’s better to see the graph below.
Now, we can use math module from Python and compute LCM. $LCM(a,b) = \frac{\vert a \vert \times \vert b \vert}{GCD(a,b)}$. How about LCM of three integers? \(LCM(a,b,c) = LCM( LCM(a,b), c) = LCM \Big( \frac{a\times b}{GCD(a,b)}, c \Big) = \frac{\frac{a\times b}{GCD(a,b)} \times c}{GCD\Big(\frac{a\times b}{GCD(a,b)} , c \Big)} = \frac{LCM(a,b) \times c}{GCD(LCM(a,b), c)}\)
Here’s the graph explaining my approach.
Here’s the code.
import math
class Solution:
def nthUglyNumber(self, n: int, a: int, b: int, c: int) -> int:
low, high = 1, 2 * 10 ** 9
a_b = a * b // math.gcd(a,b)
b_c = b * c // math.gcd(b,c)
a_c = a * c // math.gcd(a,c)
a_b_c = (a_b*c) // math.gcd( a_b, c)
def isFeasible(num):
result = (num // a) + (num // b) + (num // c) - (num // a_b) - (num // b_c) - (num // a_c) + (num // a_b_c )
return result >= n
while low < high:
mid = low + (high - low) // 2
if isFeasible(mid):
high = mid
else:
low = mid + 1
return low
Leetcode problem #1283 - Find the smallest divisor given a threshold.
Here is the problem So, again, since we are finding the smallest number that’s less than or equal to some given threshold number, we can use binary search. If you pay attention to the problems we have solved so far, in our IsFeasible() function, our return statement has greater than or equal to. In this case, it is less than or equal to. That’s the only difference. The code is pretty much the same.
class Solution:
def smallestDivisor(self, nums: List[int], threshold: int) -> int:
def isFeasible(candidate):
result = 0
for num in nums:
if num % candidate == 0:
result += (num // candidate)
else:
result += (num // candidate) + 1
return result <= threshold
low, high = 1, sum(nums)
while low < high:
mid = low + (high - low) // 2
if isFeasible(mid):
high = mid
else:
low = mid + 1
return low
Leetcode problem # 2064 - Minimized Maximum of Products Distributed to Any Store
So, I initally thought this was a variant of Min-Max problem. However, upon looking at the problem’s constraints, this problem can be solved by binary search.
- Store can be given at most one product type (and the amount can be 0).
- Given the constraint ( n: # of specialty retail stores), we will have bunch of numbers satisfying this constraint, while distributing all products.
- We can use binary search, where low = 1 and high = max(quantities).
class Solution:
def minimizedMaximum(self, n: int, quantities: List[int]) -> int:
def isFeasible(target):
count = 0
for quantity in quantities:
if quantity % target == 0:
count += quantity // target
else:
count += (quantity // target) + 1
return count <= n
low, high = 1, max(quantities)
while low < high:
mid = low + (high - low) // 2
if isFeasible(mid):
high = mid
else:
low = mid + 1
return low Leetcode problem #540 - Single Element in a Sorted Array
Here is the problem There are few things to note regarding this problem.
- The length of an array, num, is odd.
- There is only one element that has no duplicate.
- When we find the middle point ( mid = low + (high - low) // 2), the middle point’s index can be either even or odd. For instance, if we are given an array of length 11 (so starting from 0 to 10), then the mid point is 5, whereas, the mid point is 4 for an array of length 9.
- Suppose we have an array $ [1,1,2,2,3,3,4,4,5,5,6] $ The mid point is 5 with value 3. There are odd numbers of numbers in the intervals left and right to this midpoint. We check the two numbers adjacent to the mid point (so it will be nums[mid-1] and nums[mid+1]) and see, which of them is equal to nums[mid]. If we are fortunate and we have a case where nums[mid] != nums[mid-1] AND nums[mid] != nums[mid+1], then nums[mid] is the unique element and we simply return this.
- Once we check the neighboring numbers, we reduce our search space by discarding the interval. Which interval you might say? Using that example, we have nums[mid] == nums[mid-1]. This means, our subinterval [1,1,2,2,3], which has 5 numbers (so odd) can be ignored and we simply set low = mid + 1. Why? Because that left interval has odd numbers of elements and we checked that the last element, 3, is equal to our midpoint. So this means our subarray [1,1,2,2] doesn’t contain a duplicate number. Therefore, we look at the interval to the right of mid point.
Here’s the visualization. 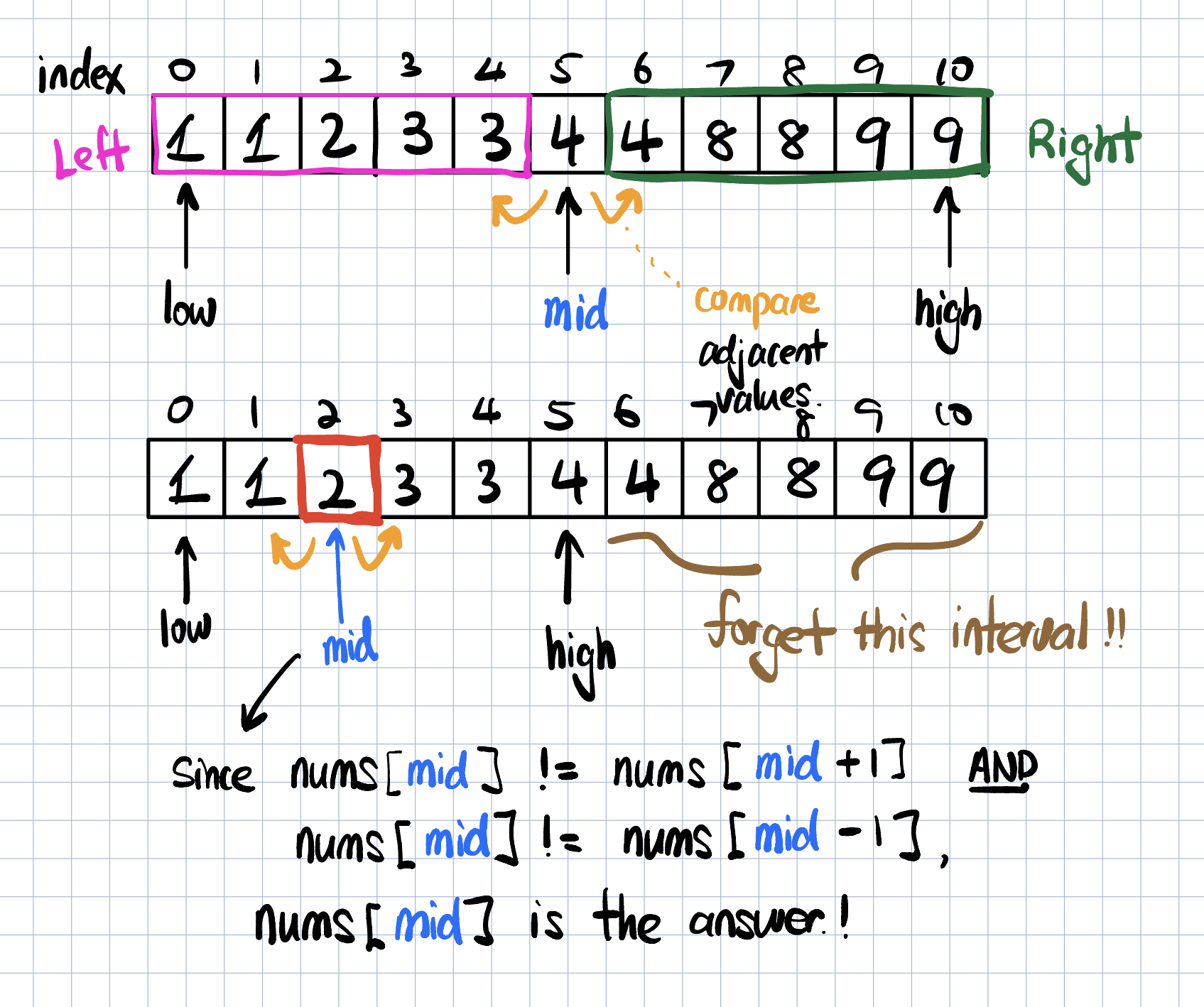
class Solution:
def singleNonDuplicate(self, nums: List[int]) -> int:
if len(nums) == 1:
return nums[0]
low, high = 0, len(nums) - 1
while low < high:
mid = low + (high - low) // 2
if nums[mid + 1] != nums[mid] and nums[mid - 1] != nums[mid]:
return nums[mid]
if mid % 2 != 0:
if nums[mid + 1] == nums[mid]:
high = mid
elif nums[mid - 1] == nums[mid]:
low = mid + 1
else:
if nums[mid + 1] == nums[mid]:
low = mid + 1
elif nums[mid - 1] == nums[mid]:
high = mid
return nums[low]
