This section contains Leetcode problems that are a bit more general than problems we have encountered so far. In other words, there are many methods to solve problems efficiently.

Leetcode Problem #2098 - Subsequence of Size K with the Largest Even Sum

Here’s the problem

How should we solve this problem? First, we can sort this array from the largest to the lowest. In some problems, sorting an array is not an ideal starting point (i.e. finding an index position of some numbers). However, in this case, we are only interested in returning the largest even sum of subsequence with length k. Because we are dealing with a subsequence, we can sort this array first.

• Now, for whatever subsequence of length k, we must have an even number. How do we get an even number? There are two cases : Even + Even = Even and Odd + Even = Even. Thus, after sorting an array, if the k largest numbers add up to an even number, we simply return this number. Otherwise, this means the sum of k largest numbers is odd. How do you get an odd number? It is Odd + Even = Odd. Thus, either (1) We have to swap Odd with Even or (2) swap Even with Odd number.
• What do I mean by this? Let’s say we sorted the array from the largest to the lowest. Assume that the sum of k largest elements is odd number. Then let’s find the lowest even and odd numbers among the k largest elements. Let’s denote them lowest_even and lowest_odd. Next, from k+1th element (in Python, our for loop will start from k), we will swap these numbers in the following way : if, say, k+1th element is even, then we (1) check first whether the lowest_odd exists. If lowest_odd exists, then we will swap lowest_odd with k+1th element. Then we update our sum (in my code, this sum is denoted by result).

class Solution:
    def largestEvenSum(self, nums: List[int], k: int) -> int:
        nums.sort(reverse = True )
        sum_k = sum(nums[:k])
        
        if sum_k % 2 == 0:
            return sum_k 
        
        lowest_even = float("inf")
        lowest_odd = float("inf")
        
        highest_even = 0
        highest_odd = 0 
        
        for i in range(0, k):
            if nums[i] % 2 == 0:
                lowest_even = min(lowest_even, nums[i])
            else:
                lowest_odd = min(lowest_odd, nums[i])
        result = -1 
        for i in range(k, len(nums)):
            if nums[i] % 2 == 0 and lowest_odd != float("inf"):
                result = max(result, sum_k - lowest_odd + nums[i])
            elif nums[i] % 2 == 1 and lowest_even != float("inf"):
                result = max(result, sum_k - lowest_even + nums[i])
        return result 

Leetcode Problem #2091 - Removing Minimum and Maximum from Array

Here is the problem

I couldn’t figure out where to put this problem, so I put it here. Once we find the maximum and the minimum of an array, nums, and their positions as well, we have 3 cases to consider.

• First case : We simply start from an index 0 and continue until we hit the maximum of index positions of those two numbers.
• Second case : We start from an index (len(nums) - 1), i.e the last index. We traverse backward until we hit the minimum of index positions of those two numbers.
• Third case : For smaller index position, we start from 0. For larger index position, we start from the end. Combine these two numbers.
• We return the minimum of (first case, second case, third case).

See the graphical solution below to help you understand my code.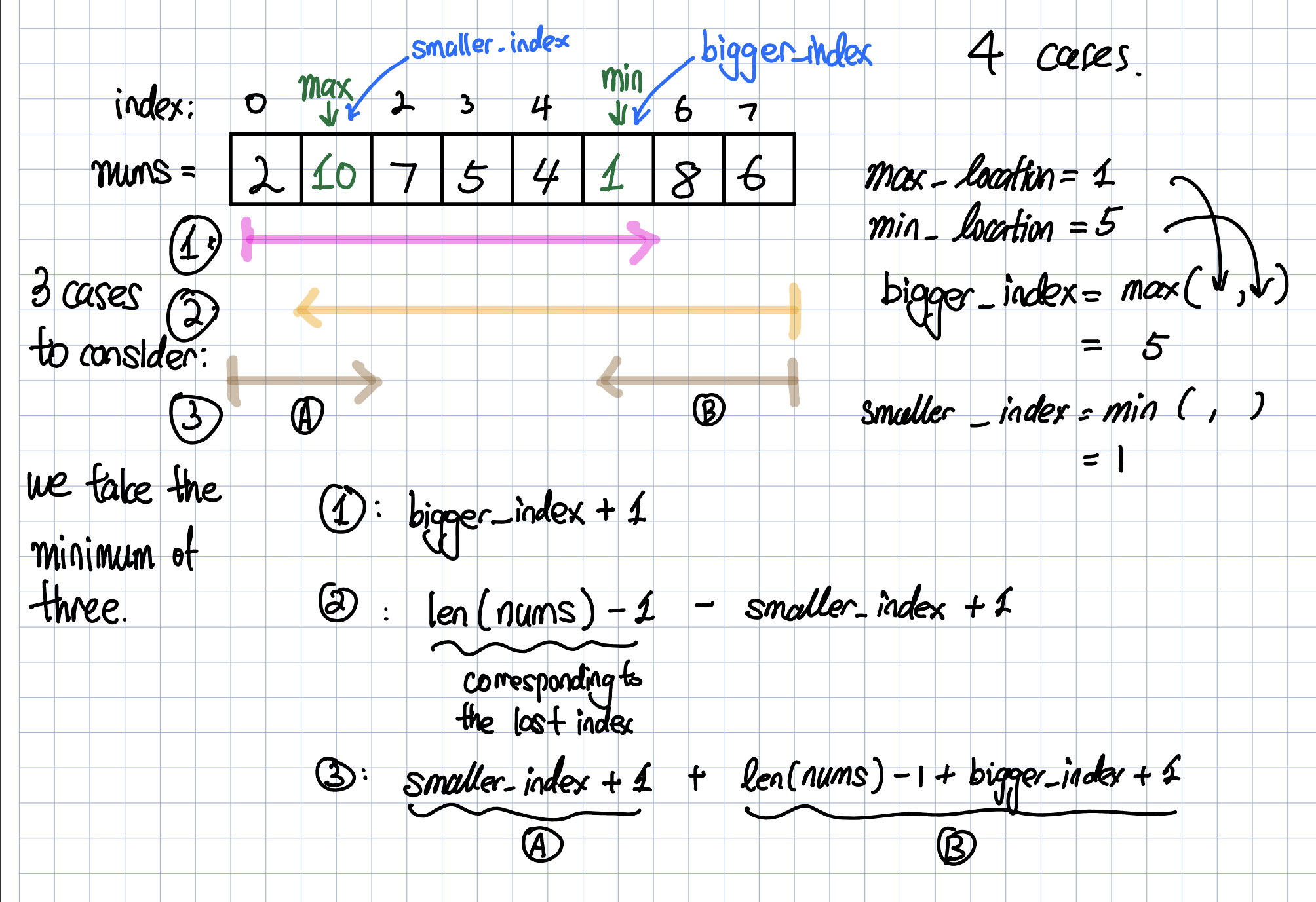

class Solution:
    def minimumDeletions(self, nums: List[int]) -> int:
        maximum, minimum = 0, 0
        n = len(nums)
        
        maximum = max(nums)
        minimum = min(nums)
        max_location = nums.index(maximum)
        min_location = nums.index(minimum)
        
        bigger_index = max(max_location, min_location)
        smaller_index = min(max_location, min_location)
        
        
        return min(bigger_index + 1, n - smaller_index , smaller_index + n  - bigger_index + 1)

Leetcode Problem #1647 - Minimum Deletion to Make Characters Frequencies Unique

Here is the problem

For this problem, the key point is that we are only making deletion. If we are allowed to have both addition and deletion, this problem could have been more difficult. Thankfully, we only care about deletion. Hypothetically, let’s say we have “aaabbbcccdddeee”. Then we can count how many these alpahbets are occuring. So we have {a : 3, b: 3, c: 3, d : 3, e : 3}. While we can use dictionary to store frequencies, I prefer an array because we only have 26 characters. Initializing an array first by setting counter = [0] * 26, we would have [3,3,3,3,3, 0,0, …, 0]. We can use a set to determine if we already have the same frequency in our set. Since our set is empty, counter[0] is not in the set so we add 3 to the set. Next, we are at counter[1]. Because this is already in our set, we decrement it by 1 and see if this reduced number is in the set. It’s not so we add 2 to the set. Our set has {3,2}. Now we are at counter[2], which is 3. Decrement it by 2 and our set is now {3,2,1}. Now how about counter[3]? This is also 3. Well, the problem’s example 3 says that frequency of 0 is just ignored. This means we can decrement this number to 0 and forget about it. If we keep how many times we are decrementing numbers, we simply return that number and we are done.

class Solution:
    def minDeletions(self, s: str) -> int:
        counter = [0] * 26
        for letter in s:
            counter[ord(letter) - ord("a")] += 1
        
        result = 0 
        hashSet = set()
        for count in counter:
            if count not in hashSet:
                hashSet.add(count)
            else:
                deletionCount = 0 
                while count and count in hashSet:
                    count -= 1
                    deletionCount += 1
                hashSet.add(count)
                result += deletionCount
        return result 
                    
            

Leetcode problem #2210 - Count Hills and Valleys in an Array

Here is the problem

My first approach solving this problem was to create another array where this new array will not have duplicate numbers. So first, as we run a linear scan on the given array, we put unique numbers we encounter into this new array. Then, we run another linear scan on this new array to find the total numbers of hills and valleys.

• Time complexity : $O(n)$. The worst case is when we have no duplicate numbers, so we are running linear scan on this given array twice i.e $O(2n) = O(n)$.
• Space complexity : $O(n)$. The worst case is when we have no duplicate numbers.

My second approach was not relying on creating new array. When we encounter duplicate numbers, we move our pointer to the last position of these duplicate numbers. In other words, if we have [2,3,3,3,3,4,…], and our pointer points to index 1, then our pointer should be moved to index 4 (which is still nums[4] = 3, and yet this is the last position of those duplicate numbers). After we determine whether those numbers of 3 is a hill or a valley, we can increment index by 1 and move directly to index 5.

See below for the visual representation.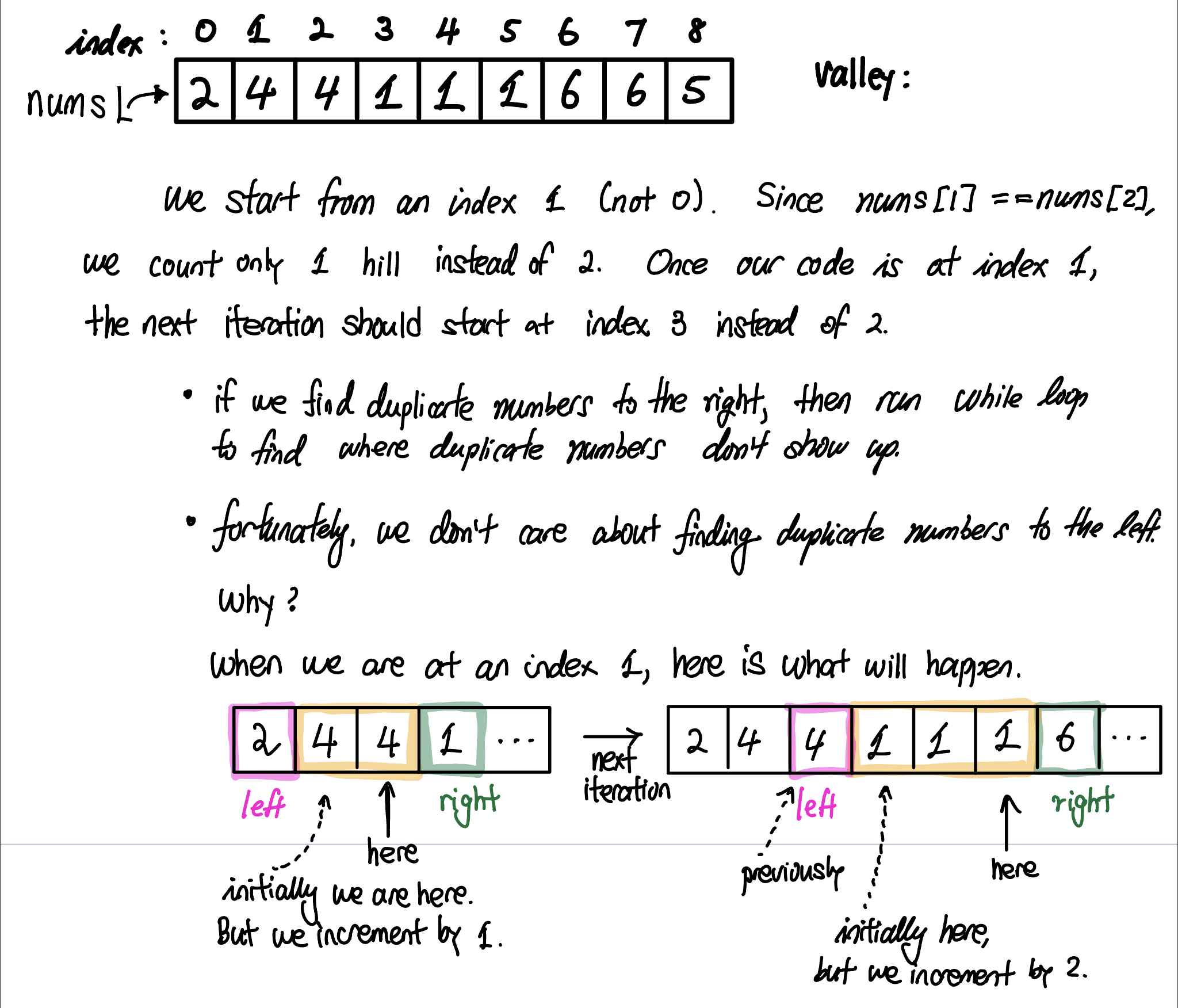

Below is the code for the first approach.

class Solution:
    def countHillValley(self, nums: List[int]) -> int:
        modified_array = []
        modified_array.append(nums[0])
        ptr = 0 
        for i in range(1, len(nums)):
            if nums[i] != modified_array[ptr]:
                modified_array.append(nums[i])
                ptr += 1
        count = 0 
        for j in range(1, len(modified_array) - 1):
            if modified_array[j-1] < modified_array[j] and modified_array[j] >  modified_array[j+1]:
                # we found a hill 
                count += 1
            elif modified_array[j-1] > modified_array[j] and modified_array[j+1] > modified_array[j]:
                count += 1
            else:
                continue 
        return count 

Below is the code for the second approach.

def countHillValley(nums):
    count = 0
    index = 1 # we start from an index 1

    while i < len(nums) - 1:
        left_number = nums[i - 1] # have to put it above inner while loop because our index i can be changed. 
        while i + 1 < len(nums) - 1 and nums[i] == nums[i + 1]:
            i += 1 
        # in the case of [2,4,4,1,...]
        # we start at index 1, which is equal to 4.
        # Our inner while loop will give us a new index, i = 2
        
        # check whether this is a hill or a valley
        right_number = nums[i + 1]
        if left_number < nums[i] and nums[i] > right_number:
            count += 1 # the case we have a hill 
        elif left_number > nums[i] and right_number > nums[i]:
            count += 1  # the case we have a valley 
        # go to the next index
        i += 1
    return count 

Next problem